Das wichtige Papierformat - DIN-A sowie das kleine und das große Einmaleins.
Zur Geschichte des DIN-A4-Papierformats
Eine verbindliche Normung der Papiergrößen z. B. für den Druck existierte vor dem Ersten Weltkrieg im damaligen Deutschen Reich nicht.
Die Normung der Papiergrößen für den Druck als DIN-Papierformate gibt es erst seit 1922 als deutsche Industrie Norm 476 und stammt daher noch aus der Weimarer Republik.
Aufgrund der industriellen Waffenproduktion im Ersten Weltkrieg zeigte sich sehr schnell das in allen Bereichen der Produktion im Reich ein starker Bedarf nach einem einheitlichen Standard für die industrielle Zusammenarbeit von verschiedenen Firmen zur Herstellung von Werkzeugen und Produkten bestand.
Daher wurde am 22. Dezember 1917 unter dem Namen „Normenausschuss“ der deutschen Industrie“ eine nationale Normungsorganisation gegründet, die aber schon 1926 zu „Deutscher Normenausschuss“ umbenannt wurde. In schneller Folge kam es zu einer regelrechten ”Normierungswelle” in Deutschland und nicht nur fast alle Gegenstände des militärischen, sondern auch die des industriellen sowie die des täglichen Bedarfs wurden nun normiert. So legte der „Normenausschuss der deutschen Industrie“ (NDI) am 18. August 1922 in der DIN-Norm 476 einheitliche Normen für Papierformate fest. Hauptverantwortlich für die 1922 entwickelte, bis heute noch gültige Normierungsreihe DIN A bis D unter der DIN 476 war als Mitglied des NDI der Ingenieur Walter Porstmann. Verbindlich wurde die Norm im Deutschen Reich aber erst ab 1923 und es zeigte sich sehr schnell, das insbesondere mit dem massenhaften Aufkommen von Schreibmaschinen sowie Fernschreibgeräten die DIN-Papierformate von extremen Vorteil waren. Bis heute sind in dieser DIN-Norm die Vorzugsreihe DIN A (beschnittenes Format) sowie die Zusatzreihen DIN B (unbeschnittenes Format) und DIN C (für Versandhüllen) festgelegt und bis auf die D-Reihe gültig. Die Formate der A-Reihe haben das Seitenverhältnis 1 zu Wurzel aus 2 - also, dass Flächenverhältnis lautet, 1:2, je 2 benachbarte Formate ergeben sich daher immer durch halbieren oder verdoppeln. Das oft genutzte Format A4 ist die Hälfte von A3, aber das Doppelte von A5. Das Ausgangsformat A0 hat 1 Quadratmeter Flächeninhalt mit einer Seitenlänge von 841 mm zu 1189 mm. Also ein Rechteck von 1 m² Flächeninhalt. Die Formate der Hauptreihe A gelten für alle unabhängigen Papiergrößen (Geschäftsbriefe, Zeitschriften u. a.). Die Formate der Nebenreihen B und C gelten für alle abhängige Papiergrößen (Briefhüllen, Bücher, Mappen, Aktendeckel u. a.). Alte Papierformate wie Kanzlei, Oktav und Quart findet man heute nur noch im Kunstdruck oder auf Bestellung. Die deutsche Norm 476 diente dabei mit ihren Festlegungen über die A- und B-Reihe als Grundlage für den europäischen beziehungsweise internationalen Standard für Papierformate ISO 216, der wiederum in fast allen Ländern übernommen worden ist, aber es gibt oft Unterschiede in den erlaubten Toleranzen.
Seit 1975 heißt der Normenausschuss nun „DIN Deutsches Institut für Normung e. V.“ und ist ein eingetragener Verein, der sich privatwirtschaftlich trägt, aber er wird von der Bundesrepublik Deutschland als einzige nationale Normungsorganisation unterstützt. Das Institut bietet den sogenannten „interessierten Kreisen“ (Handel, Hersteller, Industrie, Wissenschaft, Verbraucher, Prüfinstitute und Behörden) ein Forum, um im Konsensverfahren Normen zu erarbeiten. Die unter der Leitung von Arbeitsausschüssen erarbeiteten Normen dieser Normungsorganisation werden als DIN-Norm bezeichnet.
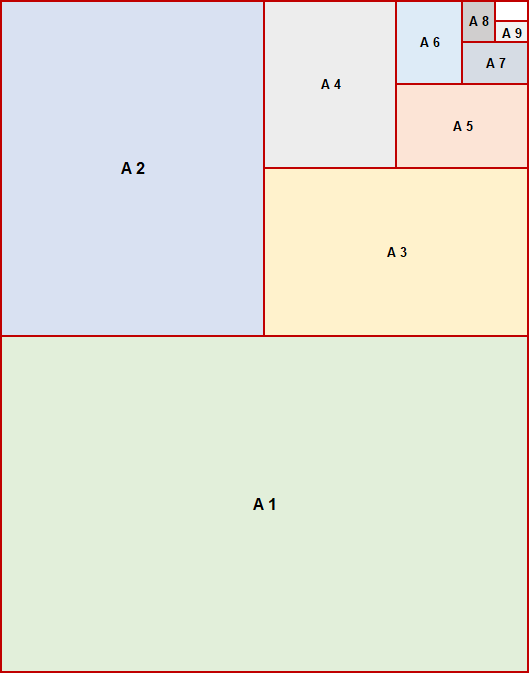
| DIN-Format | Bezeichnung | Fläche | Flächeninhalt in mm² | Fläche in Zoll |
|---|---|---|---|---|
| DIN-Format A 0 | Vierfachbogen | 841 mm x 1189 mm ( Landkarten, Wahlplakate ) | 999.949 | 33,11" x 46,81" |
| DIN-Format A 1 | Doppelbogen | 594 mm x 841 mm ( Geschenkpapier, Plakate ) | 499.554 | 23,39" x 33,11" |
| DIN-Format A 2 | Bogen / Einfachbogen | 420 mm x 594 mm ( Filmplakate, Poster ) | 249.480 | 16,54" x 23,39" |
| DIN-Format A 3 | Halbbogen | 297 mm x 420 mm ( Zeichnungen, Zeitschriften ) | 124.740 | 11,69" x 16,54" |
| DIN-Format A 4 | Viertelbogen (Briefbogen) | 210 mm x 297 mm ( Schulheft, Briefpapier ) | 62.370 | 8,27" x 11,69" |
| DIN-Format A 5 | Achtelbogen (Blatt) | 148 mm x 210 mm ( Broschüren, Notizblöcke, Karteikarten, Kleines Schulheft ) | 31.080 | 5,83" x 8,27" |
| DIN-Format A 6 | Halbblatt | 105 mm x 148 mm ( Post- und Grußkarten, Taschenbücher ) | 15.540 | 4,13" x 5,83" |
| DIN-Format A 7 | Viertelblatt | 74 mm x 105 mm ( Taschenkalender, Spielkarten, Foto-Sticker ) | 7.770 | 2,91" x 4,13" |
| DIN-Format A 8 | Achtelblatt | 52 mm x 74 mm ( Chip- und Visitenkarten, Etiketten ) | 3.848 | 2,05" x 2,91" |
| DIN-Format A 9 | - | 37 mm x 52 mm ( Passfoto ) | 1.924 | 1,46" x 2,05" |
| DIN-Format A 10 | - | 26 mm x 37 mm ( Brief- und Wertmarken ) | 962 | 1,02" x 1,46" |
◄ Zurück zu Home Zur Themen Auswahl ▲ Glossar ►
Punkte (pt) und Pica (pc).
Punkte und Pica sind die typographischen Maßeinheiten mit dem Designer am ehesten vertraut sind, da besonders Printmedien vor allem mit dieser Einheit arbeiten.
Das erste typographische Punktsystem wurde von Sébastien Truchet (*1657 - † 1729) einem französischer Priester und Erfinder konzipiert. Sein Punkt betrug genau 1/1728 „pied du Roi” (Fuß), also etwa 0,188 mm und entspricht somit genau der Hälfte des späteren Didot-Punktes. Vater Sébastien gilt als der Erfinder der Schriftart Romain du Roi, auf deren Prinzip heute viele Vektorschriften beruhen.
Etwa seit 1737 verwendete der französische Drucker Pierre Simon Fournier einen eigenen typographischen Punkt. Er betrug etwa 0,345 mm, also etwa elf Zwölftel spätere Didotpunkte. Der sogenannte Fournier-Punkt wurde dann nicht weiterverwendet.
Weiterentwickelt wurde das Maßsystem Ende des 18. Jahrhunderts von François Ambroise Didot und seinem Sohn Firmin Didot.
Der Didot-Punkt, der sich dann auch praktisch in ganz Europa durchsetzte, betrug traditionell 0,376065 mm (nach offizieller Umrechnung aber etwa 0,3759715 mm). Er wird üblicherweise mit 0,376 mm angegeben und auch so verwendet (mit + 0,0173 % bzw. - 0,0075 %, weit innerhalb aller technischen Toleranzen). Das Grundmaß war der Fuß, das alte französische Längenmaß Pied de roi. So entsprechen 6 x 12 x 12 = 864 Didotpunkte genau einem französischen Fuß.
Der Punkt (p) ist die Grundeinheit zur Angabe von Schriftgrößen.
1 Punkt entspricht 1/72 Zoll (Inches), wobei 1 Zoll = 2,54 Zentimeter ist, 1 Pica entspricht 12 Punkten.
Punkte (Points) sind im Web aber bedeutungslos - sie sind eine Einheit für den Druck, nicht für den Bildschirm. Um Punkte auf dem Bildschirm darstellen zu können, müssen sie in Pixel umgerechnet werden. Dies geschieht anhand der ppi Zahl (Pixel Pro Zoll). Diese Zahl kann sehr unterschiedlich sein.
Auf Windows Systemen kann man sie konfigurieren, bei „kleinen Schriftarten” sind es 96ppi und bei „großen Schriftarten” sind es 120ppi aber auf dem MacOS sind es nur 72ppi. Eine 9pt große Schrift würde also auf dem Macintosh 9 Pixel groß sein, auf einem Windows System 12 Pixel oder 15 Pixel. Ist eine Schrift auf einem Windows System noch lesbar, ist sie auf dem Macintosh nicht mehr zu entziffern.
Typographische Maßsysteme
Alle Maße auf der Welt basieren heute auf dem metrischen Maßsystem.
Alle Maßsysteme?
Nein, nur ein kleines Fachgebiet wehrt sich entschieden gegen diese Vormacht:
Die Rede ist vom Typographischen Maßsystem, im Jahre 1737 von dem Pariser Schriftengießer Pierre Simon Fournier entwickeltes Punktsystem, diente dazu eine einheitliche Basis zu finden für die Schriftherstellung.
Die kleinste typographische Maßeinheit ist der Punkt (Abkürzung: p).
1 Konkordanz = 4 Cicero (Abkürzung: c)
1 Cicero = 12 p
1 Petit = 8 p
1 Nonpareille = 6 p
Im Vergleich vom typographischem Maß mit dem metrischen Maß ergibt sich:
1p = 0,376 mm
1mm = 2,66p
1 Cicero =4,512 mm
1979 hat der Bundesverband Druck beschlossen, die Maße zu runden, so dass sie immer auf 0 oder 5 enden müssen, demnach entspricht
1 p = 0,375 mm
1 Cicero = 4,5 mm
Im angelsächsischen Raum hat sich das Point-System durchgesetzt, indem 1 Point (Abkürzung: pt) = 0,351 mm ist. Die nächstgrößere Einheit ist das Pica, das 12 pt enthält ca. 4,23 mm (ich weiß rechnerisch sind es 4,212 mm, aber ich denke mir das da auch gerundet wird); 1 Inch = 6 Pica.
Um die Verwirrung komplett zu machen, gibt es noch den DTP-Point, der dem Point-System entstammt, aber in dem 1 pt = 0,352 mm sind. Außer bei den Schriftgrößen und dem Zeilenabstand wird das Typographische Maßsystem nicht mehr angewendet. Positionen und Maße von Bildern usw. werden heute alle in mm angegeben.
Übrigens darf in der deutschen Rechtschreibung das französische Wort Typographie auch eingedeutscht mit "f" als Typografie geschrieben werden.